When project risks don’t add up
The way PMI deals with risk in the PMBOK® Guide is simplistic. Calculating the effect of one risk using the suggested probability x severity calculation provides one value. For example, if there is an 20% probability an estimate is undervalued by $50,000, the Expected Monetary Value (EMV) for this event will be:
-$50,000 x 0.2 = -$10,000
It is simple, but not a lot of use in the real world.
The first problem is the underestimated value is not known and would be better represented by a range statement but as the values in the range alter, so does the probability of and value occurring. Thinking of your car for a moment:
- There is a fairly high probability of an accident causing a minor scratch or dent occurring in any given year (particularly in shopping centre car parks), say a 20% probability of an accident occurring with the damage costing $500 or less to repair.
- There is a very low probability of an accident causing the car to be written off; say a less then 1% chance of an accident costing $50,000 or more.
While there is only one car and it may have more than one accident in a year, these parameters do not mean there will ever actually be an accident. Even the 20% probability of a $500 accident occurring in any given year, does not mean there will be at least one accident every five years. The maths is much more complicated.
The next issue is correlation. Returning to the underestimate, was the underestimate a one-off factor (caused by a single unrelated external supplier) or is it a systemic estimating error affecting a number of related estimates (possibly caused by changes in the exchange rate). This needs modelling to determine the overall effect.
Then we come to the purpose of this article: do risks add together or discount each other? It depends on the situation.
Situation 1 looks at the probability of starting on time.
Consider three schedule activities each of 10 days duration, all of which need to be complete before their outputs can be integrated.
Activity 1 and 2 both have a 90% probability of achieving the estimated duration of 10 days. Activity 3 has an 80% probability of achieving the 10 days.
The overall chance of starting the ‘Integration’ activity on schedule needs an understanding of how these three activities affect its start. Based on the percentages above:
- Activity 1 has a 1 in 10 chance of causing a delay
- Activity 2 has a 1 in 10 chance of causing a delay
- Activity 3 has a 1 in 5 chance of causing a delay
There are 10 x 10 x 5 = 500 possible outcomes within the model and within this
9 x 9 x 4 = 324 ways of not being late (it does not matter how early any of the projects finish as long as they are not late).
Take the number of ‘not late’ outcomes from the possible range of outcomes:
- 500 – 324 leaves 176 ways of being late
- 176/500 = 0.352 or a 35.2% probability of not making the start date
- Or a 100 – 35.2 = 64.8% probability of being on time
The quicker way to calculate this is simply to multiply the probabilities together for 0.9 x 0.9 x 0.8 = 64.8%
For a more complete explanation, see What’s the probability?
Situation 2 looks at the probability of finishing on or under budget.
In this scenario, money saved on one part of the project can be used to offset overspending on another. Assume you have 10 teams working on your project and they all estimate completing their section of the work for between $8,000 and $12,000; with the expected average of $10,000 per team. As the project manager, you can aggregate these estimates to arrive at a project budget of $100,000.
However, your team leaders are unlikely to submit an estimate which only has a 50% chance of being achieved—let’s assume they use the 90% probability benchmark common in oil and gas projects.
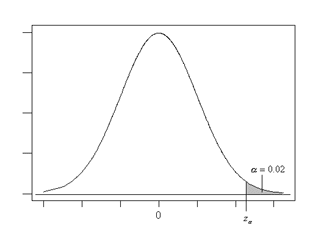To achieve a 90% probability of the estimate being achieved, each of the individual team estimates will need to be increased to around $11,300 (assuming a normal distribution), which pushes the overall project budget up to $113,000 if you simply add up the risk adjusted estimates.
If you accept this approach, how much safety does this give the project manager? The answer is a surprising 99.998% probability of not exceeding the overall project budget!
The effect of combining uncertainties into a ‘portfolio’ is to reduce the overall level of uncertainty in the portfolio; basically wins on the ‘swings’ can be used to offset losses on the ‘roundabouts’ generating an increase in the overall probability of achieving any given target for the portfolio.
So if your project needs to achieve a 90% certainty overall and there are 10 separate teams, the correct budget is around $104,000, not the $113,000 calculated by summing each of the teams ‘90% estimates’ or the $113,000 required if the project is a single holistic entity. For more on this see Averaging the Power of Portfolios.
Confused or worried? I hope this has made you think about getting serious help when you start looking beyond developing a simple risk register. The difference between an individual project’s risks, the overall risk of a project and the risks associated with a portfolio of projects are complicated.
