Measuring project uncertainty

Latin hypercube sampling (LHS)
LHS is a statistical method for generating a sample of plausible collections of parameter values from a multidimensional distribution. It was described by McKay in 1979. An independently equivalent technique was proposed by Eglājs in 1977. And it was further elaborated by Ronald L Iman, and others in 1981.

Latin Hypercube sampling stratifies the input probability distributions and takes a random value from each interval of the input distribution. The effect is that each sample (the data used for each simulation) is constrained to match the input distribution very closely. Therefore, for even a modest sample sizes, the Latin Hypercube method makes all, or nearly all, of the sample means fall within a small fraction of the standard error. This is usually desirable.

(In the context of statistical sampling, a square grid containing sample positions is a Latin Square if (and only if) there is only one sample in each row and each column. A Latin Hypercube is the generalisation of this concept to an arbitrary number of dimensions, whereby each sample is the only one in each axis-aligned hyperplane containing it.)

Different types of sampling
The difference between random sampling, Latin Hypercube sampling and orthogonal sampling can be explained as follows:

1. The Monte Carlo approach uses random sampling; new sample points are generated without taking into account the previously generated sample points. One does thus not necessarily need to know beforehand how many sample points are needed.
2. In Latin Hypercube sampling one must first decide how many sample points to use and for each sample point remember that it has been used. Fewer iterations are needed to achieve convergence.
3. In Orthogonal sampling, the sample space is divided into equally probable subspaces. All sample points are then chosen simultaneously making sure that the total ensemble of sample points is a Latin Hypercube sample and that each subspace is sampled with the same density.

In summary orthogonal sampling ensures that the ensemble of random numbers are a very good representation of the real variability but is rarely used in project management. LHS ensures that the ensemble of random numbers is representative of the real variability whereas traditional random sampling is just an ensemble of random numbers without any guarantees.

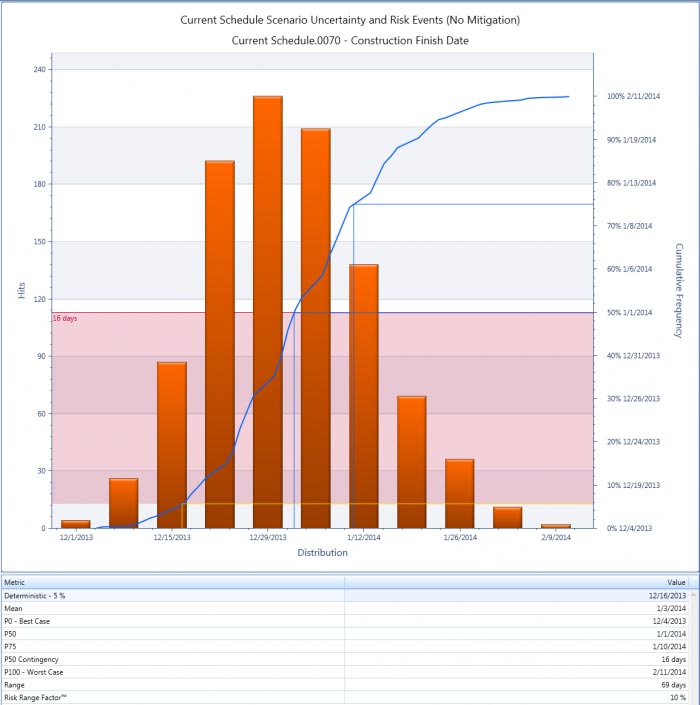
The results

Image: Snapshot from Acumen Risk, a cost and schedule risk analysis tool

Once you have a reliable probability distribution and a management prepared to recognise, and deal with, uncertainty you are in the best position to effectively manage a project through to a successful conclusion. Conversely, pretending uncertainty does not exist is an almost certainly a recipe for failure!

In conclusion, it would also be really nice to see clients start to recognise the simple fact there are no absolute guarantees about future outcomes. I am really looking forward to seeing the first intelligently prepared tender that asks the organisations submitting a tender to define the probability of them achieving the contract date and the contingency included in their project program to achieve this level of certainty. Any tenderer that says they are 100% certain of achieving the contract date would of course be rejected based on the fact they are either dishonest or incompetent.